Efni vinnusmiðjunnar
Í þessari vinnusmiðju vinnum við með teninga til að skoða líkindafræði. En því líkindafræði hljómar háfleygt skulum við byrja á hugtaki sem við höfum öllu betri tilfinningu fyrir: Heppni.
Hér á síðunni eru nokkrar æfingar sem þið getið gert til að undirbúa heimsóknina í Vísindasmiðjuna. Samhliða þeim getur verið áhugavert að ígrunda og ræða:
- Hvað er heppni?
- Eru sumir heppnari en aðrir?
- Hvað á heppni skylt við vísindi?
Jú, við getum notað vísindi til að skilja heiminn og þar sem upplifanir okkar eru af heiminum, getum við skoðað þær. Heppni getum við t.a.m. mælt með því að skrá hjá okkur atvik.
Verkefni
Teningakast með einum tening
Skiptið ykkur niður í pör. Fyrir þessa æfingu þarf hvert par:
- Einn tening
- Skriffæri og rúðustrikað blað, eða töflureikni á tölvu
Gerið töflu líkt og þessa hér til hliðar og skráið hversu oft hver hlið kemur upp á teninginum.
Áður en þið kastið teninginum skulið þið ræða hversu oft þið teljið að hver tala muni koma upp og af hverju. Hversu ólíkar þyrftu mælingarnar ykkar að vera til að þið munduð segja að tilgátan ykkar hafi ekki staðist?
Kastið teninginum 20 sinnum, skráið niðurstöðurnar og gerið stöplarit af þeim. Stenst niðurstaðan?
Kastið tengingnum minnst 60 sinnum, skráið niðurstöðurnar og gerið stöplarit eins og fyrr. Breyttist eitthvað? Berið niðurstöðurnar saman við niðurstöður hinna. Eru þær eins? Af hverju/af hverju ekki?
Teningakast með tveimur teningum
Þessi æfing er sambærileg hinni að ofan nema nú þurfa pörin tvo teninga hvert. Það er svosum hægt að kasta einum teningi tvisvar, en það getur hjálpað sumum talsvert að sjá báðum kastað í einu upp á skilning.
Athugum sumsé hvernig þetta lítur út fyrir summu tveggja teninga. Þ.e.a.s. köstum tveimur teningum, leggjum saman fjölda doppa á hliðunum og skráum í töflu eins og áður. Athugum að lægsta mögulega summan er 2 og sú hæsta 12 en annars er taflan sambærileg og áður.
Rétt eins og áður skulum við setja fram tilgátu hvað kemur út. Hvaða niðurstaða teljið þið að verði líklegust?
Kastið aftur 20 sinnum (20 pörum af teningum), skráið hjá ykkur og búið til stöplarit. Stenst tilgátan ykkar?
Kastið svo 60 sinnum, skráið hjá ykkur niðurstöðurnar og búið til stöplarit. Berið niðurstöðurnar ykkar saman við niðurstöður hinna. Eru þær samhljóða?
Úrvinnsla og umræður
Við höfum það oft á tilfinningunni að slembin (e. random) kerfi eigi að hafa nokkuð jafna dreifingu. Til að mynda eigi teningur að gefa að jafnaði jafn oft tvist eða þrist eins og sexu. Sem er vissulega rétt, en þessi jafna dreifing getur verið nokkuð lengi að koma í ljós.
Eflaust voru sumir með umtalsvert fleiri köst af einni tölu en annarri. Í einni keyrslu á eins teninga kasti sem taldi alls 80 köst, komu þristar oftast upp, eða 23 sinnum, og fjarkarnir sjaldnast, eða 12 sinnum. Munurinn var tvöfaldur!
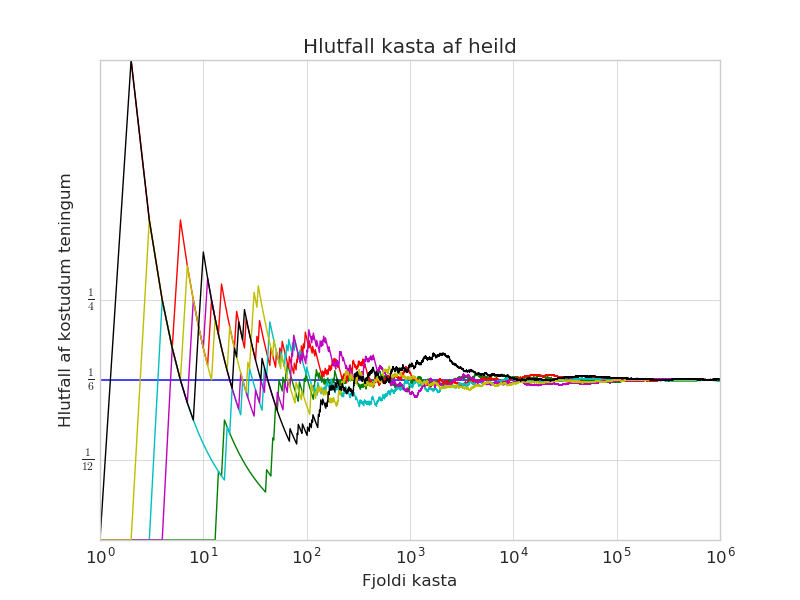Það er áhugavert að fylgjast með þessari þróun og sjá eina töluna taka „forystu“ og aðra síðar ná henni og jafnvel taka framúr. Allt eru þetta þó jafn líkar tölur.
Okkur þykir þetta mörgum merkilegt fyrir það hvað jafna drefingin er lengi að koma í ljós. Með fáum köstum munu sumar útkomur vera mun algengari en aðrar (jafnvel margafalt) en með síendurteknum köstum munu þau jafnast út.
En hvað segir þetta okkur um heppni: Jú, þótt okkur þyki ein útkoma standa á sér (t.d. sexan í Lúdó) eða óheppni í einhverju lífsins spili, þá er það einfaldlega eðli slembinna ferla, að sjaldan fellur ein báran stök.
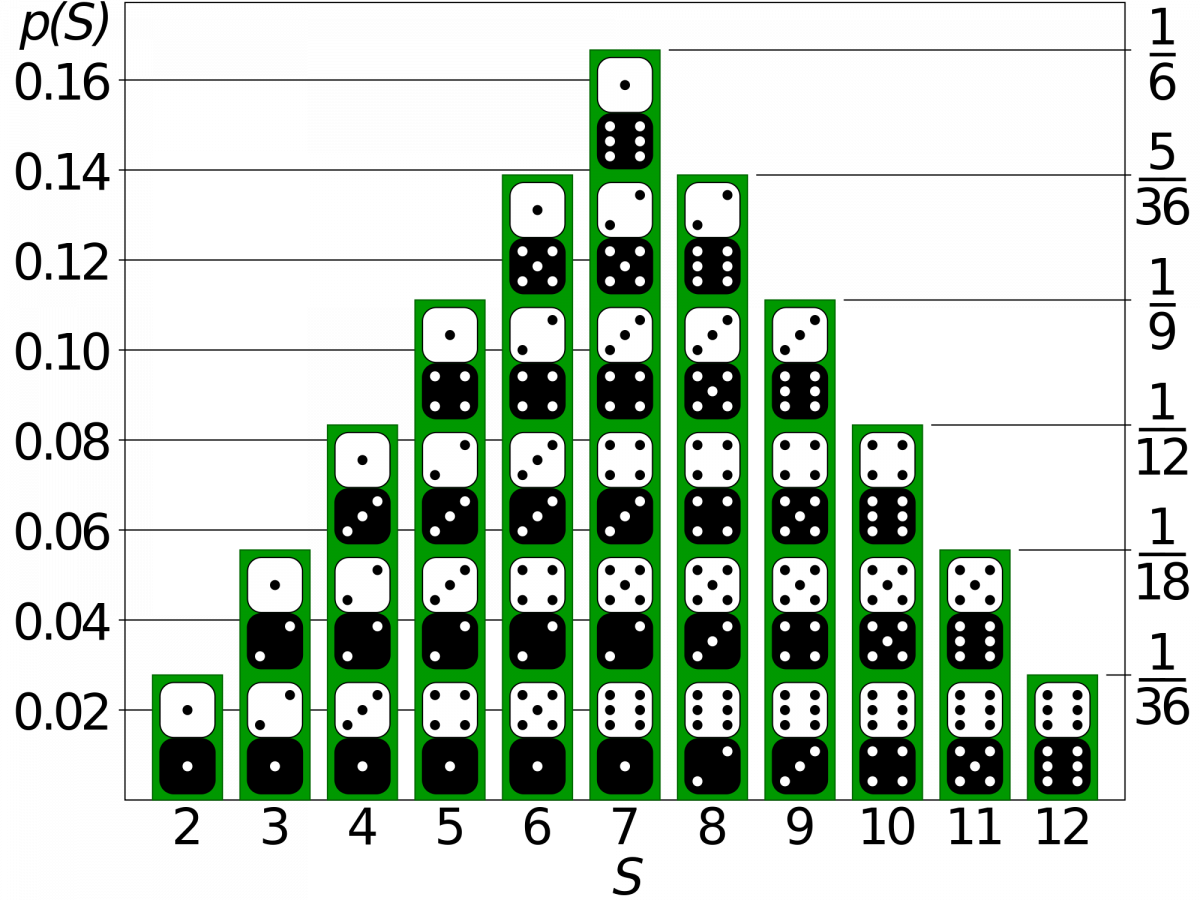
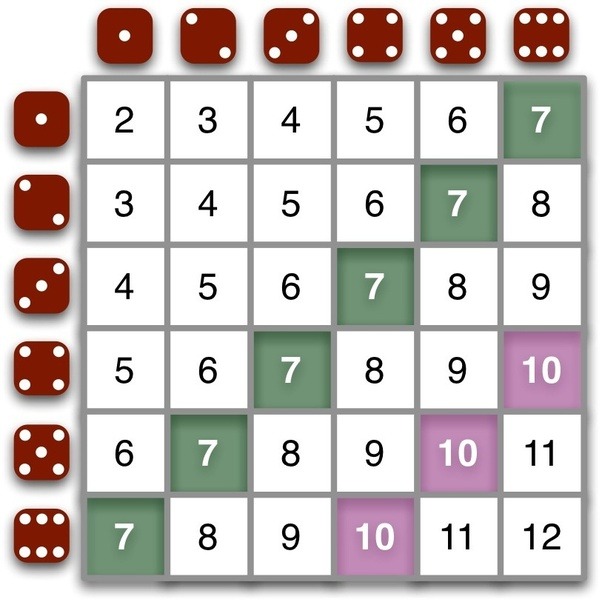
Tveggja teninga kastið er sömuleiðis áhugavert. Með því að blanda saman tveimur einföldum slembnum ferlum getum við fengið afdráttalaust mynstur.
Ólíkleg teningaköst
Við höfum sumsé séð að sumar niðurstöður eru ólíklegri en aðrar.
Hversu líklegt er að fá eina sexu? En tvær? Hvað með þrjár og fjórar?
Hversu oft þurfum við að kasta til að það séu 50% líkur á því að hafa kastað sexu? En 100%?
Hversu oft þurfum við að kasta til að það séu 50% líkur á því að hafa kastað tveimur sexum?
Forritun teningakasta
Það má spara sér nokkra handavinnu (en þá missir maður af því að kasta haug af teningum, sem er náttúrulega gaman) með því að búa til forrit sem kastar teningum fyrir mann í gríð og erg. Hér að neðan eru tvö dæmi sem nota Scratch og P5.js.
Scratch
Fyrir þau sem eru að stíga sín fyrstu skref í forritun getur verið þægilegt að nota kubbaforritunarviðmót eins og Scratch. Verkefnið hér að neðan líkir eftir teningakasti. Hægt er að núllstilla teljarana með því að slá á „0“ á lyklaborðinu, kasta einum teningi með því að smella á græna hringinn, og (til að spara sér músarsmellina) hundrað teningum með því að slá á bilslána. Kóðann má nálgast hér.
P5.js
Þau sem eru komið aðeins lengra geta leikið sér með Processing (sem byggir á Java) eða vef-lægu útgáfunni p5.js (sem byggir á Javascript og getur keyrt í vafra).
Verkefnið hér að neðan líkir eftir stöðugu tengingakasti. Það er ræst með því að smella á gráa flötinn og er hægt að gera hlé með því líka. Rauða línan sýnir meðaltal teningakastanna. Kóðann má nálgast hér.